Seeing Without Looking: The Quantum Bomb

Some of the most dramatic and unintuitive experimental results in quantum mechanics have come from dedicated physicists’ insistence on pushing the bounds of what should be physically possible (but not all, as Henry Becquerel’s serendipitous discovery of radioactivity reminds us). Dedication to probing the strangeness of quantum physics has been paying off for over a hundred years.
One of the more recent and striking successes of quantum theory, first posited in 1993 by Avshalom Elitzur and Lev Vaidman of Tel Aviv University, is the idea that we can actually detect an object without using photons or any other particles to look at it. What in the world does that mean? Well,

Imagine you’re tasked with determining whether a new (highly classified) special “quantum bomb” is operational or is a dud. This quantum bomb has two characteristics that make it extremely volatile:

1. If the bomb is operational, it will explode when a single photon of light strikes it;
2. If the bomb is a dud, it will not interact with photons in any way.

This may be an extremely strange and dangerous bomb, but you’ve found yourself before a problem which seems impossible: any light you shine on the bomb, perhaps to test it, will just cause an explosion. How can you possibly test that the bomb works without causing it to explode?

You need to perform an interaction-free measurement.

All familiar forms of measurement involve some physical interaction. When your eye or a camera sees an object, it is seeing photons which have interacted with the object you are observing—they have been scattered by its surface. It seems there’s just no way around having some sort of physical interaction involved in measuring something—be it a chemical reaction allowing you to smell, or absorption and reflection of photons on a basketball’s surface. (That’s not quite true, actually: some other touch-free measurements do exist. You can locate a nucleus by shooting protons at it and observing their deflection in the electric field surrounding the nucleus, and you can prove that your lost keys are under the sofa if you check everywhere else and don’t find them. In both of these cases, though, you have to know something about the object you’re trying to observe–like the fact that the keys must exist somewhere–in order to make a “measurement.”)

But a fascinating alternative form of measurement exists which requires no prior information whatsoever about the object to be detected. With interaction-free measurements (IFMs), you can “see” the quantum bomb without even “looking”, in the sense that you need not cause any photons to interact with the bomb in order to detect it. I’ll sketch out a couple thought experiments that show how an IFM works.

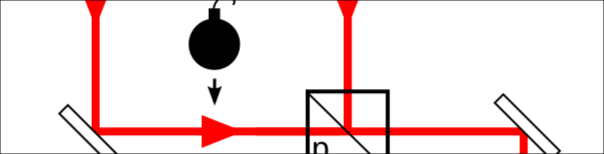
Suppose you’ve set up an interferometer made up of two beam-splitters (each with 50% transmittance), two mirrors, and two photon detectors D₁ and D₂, arranged as in Figure 1.

Figure 1. An incoming photon may traverse either path 1, path 2, or both paths through the interferometer, depending on the observation scheme.

The lengths of path 1 and path 2 are tuned to be exactly equal. If paths 1 and 2 are unobstructed, the wave-nature of incoming photons will cause interference between the two paths through the interferometer—analogous to the interference seen in Young’s double-slit experiment (where paths 1 and 2 would correspond to paths through each of the two slits, respectively). The photon detectors D₁ and D₂ are positioned so that D₁ detects all the outgoing photons (like Young’s bright fringes) and D₂ observes no photons at all (like Young’s dark fringes). If you want more persuasion to see why interference causes only one of the detectors to ever fire, take a look at the technical aside.

Technical Aside

Following the description in the original paper by Elitzur and Vaidman [1], call the quantum state of a photon traveling horizontally and that of a photon traveling vertically . A mirror will change the direction of a photon from horizontal to vertical (or vice versa), and introduce a phase shift to the state (check out the explanation on page 6 of the problem set in Ref. [2] for an explanation of why the phase-shift on reflection is  ). So a mirror acts like:

Additionally, a beam-splitter will produce a superposition of a horizontal state and a vertical state:

The s come from unitarity, meaning essentially that the total amplitude of the resulting state should be 1. Looking at Figure 2, follow each path through the interferometer and check the operation of each element with the operational descriptions above. You’ll see that if the upper- and lower-path lengths are tuned to be equal, the upper beam-splitter operates like , which is just a horizontally-traveling photon state with a phase-shift of relative to the incoming state. So the outgoing state has no vertical component, and D₂ won’t observe any photons.

Figure 2. The states corresponding to photons in each branch of the interferometer cause constructive interference at D₁ and destructive interference at D₂.

——

So for any photon you let into the interferometer, you know detector D₁ is going to fire.
Now suppose you place your quantum bomb somewhere in path 2. If the bomb is operational, no photons can possibly complete path 2 without exploding the bomb, so no interference can occur. Photons will behave more like particles. If the bomb is a dud, it doesn’t interact with the photon at all, so the situation is just like it was when the bomb wasn’t obstructing path 2.
What happens to an incoming photon if there is an operational bomb in path 2? At the first beam-splitter, a photon has a probability of ½ to take the upper path and strike the bomb. If the photon takes the lower path, it once again has a probability of ½ to be either reflected (and sent to D₁) or transmitted (and sent to D₂) by the second beam-splitter. So about 50% of the photons will take path 2 and hit the bomb, and the other 50% will be evenly divided between reaching D₁ and D₂. This means that if we fire an individual photon into the setup containing a functional bomb, D₂ will fire with a probability of ¼. If D₂ does fire (which, remember, cannot happen unless the bomb is operational), we have determined that an operational bomb is present in the system without exploding it. If D₁ fires, we haven’t learned anything, since D₁ will always fire if the bomb is a dud and will sometimes fire if the bomb is operational. That’s great, but we’re still stuck with blowing up the bomb 50% of the time and learning nothing 25% of the time. If you repeated the experiment 100 times with 100 operational bombs, about 50 bombs would explode, about 25 operational bombs would be found to be present without exploding, and about 25 cases would be totally mysterious. We can force physics to do better than that.

Mark A. Kasevich of Stanford University proposed a method for successfully making such an interaction-free measurement much more than 25% of the time. An illustration of the idea uses two polarizing beam-splitters, which transmit horizontally-polarized light and reflect vertically-polarized light, a polarization rotator, and two switchable mirrors arranged as shown in Figure 3. A horizontally (H)-polarized photon is allowed to enter the setup through a switchable mirror at the bottom left. Let’s say the polarization rotator rotates the polarization by 15° toward the vertical.

Figure 3. An incoming H-polarized photon cycles through the outer mirrors in the setup, passing through a polarization rotator and a beam-splitter-interferometer (consisting of the two beam-splitters and two mirrors in the upper-right corner of the diagram) during each lap. After a predetermined number of cycles (here, N=6), the photon is allowed to leave the setup through the switchable mirror in the bottom right. The polarization of the outgoing photon is then observed.

First, what happens to an incoming H-polarized photon entering the system when there’s no bomb involved? The photon (polarization) will be rotated 15° toward the vertical, then follow both arms of the beam-splitter-interferometer, and then repeat the cycle until it’s rotated to be fully V-polarized. Here the beam-splitters separate and recombine the horizontal and vertical components of the photon, but the interference effect is exactly analogous to that of the interferometer in Figure 1. After 90°/15° = 6 cycles, we switch off the switchable mirror and let the photon exit. If we measure its polarization, we will always observe vertical polarization.

Now for the interesting part: what if an operational bomb is placed in the lower leg of the beam-splitter-interferometer? An incoming H-polarized photon will be rotated 15° toward the vertical before coming upon the upper beam-splitter. The photon cannot interfere with itself, since one path is obstructed, so it must choose either the upper or the lower path. What is the probability for each choice? Well, Malus’ Law tells us the photon has a probability to be transmitted (and thereby become H-polarized) and of being reflected. If the photon is reflected, it causes the bomb to explode. If the photon is transmitted, however, it must be H-polarized (since it passed an H-polarizing splitter), so it passes through the lower beam-splitter with certainty. The process repeats, and let’s say we let the photon exit at the switchable mirror after 6 cycles. The odds that the photon survives through 6 cycles without striking the bomb are just . If the photon doesn’t survive 6 cycles, the whole experiment is reduced to rubble. If we measure the outgoing photon’s polarization, it must be horizontal, since it passed an H-polarizing splitter. But remember that if no bomb were involved (or if the bomb were a dud and couldn’t obstruct the lower path of the beam-splitter-interferometer), the outgoing photon’s polarization would always be vertical. So if we place a bomb in the setup and perform the experiment, we will get one of three outcomes:

1. An explosion.
2. An H-polarized outgoing photon, meaning the bomb is operational.
3. A V-polarized outgoing photon, meaning the bomb is a dud.

If we assume that the bomb is operational, the respective probabilities of these outcomes are:

1. .
2. 
3. .

Case 2 is the successful IFM, and its probability can theoretically be made arbitrarily close to 1 by increasing the number of cycles N (which means decreasing the polarization rotator’s rotation angle from 15° to 90°/N). If the photon could run 1000 cycles through the setup, the probability of a successful IFM climbs to over 99.75%.

The fact that nature allows us to push the probability of an interaction-free measurement arbitrarily close to 1 (in theory) is astonishing—it’s contrary to all of our everyday experience with making measurements. It means that the universe has at least one way of allowing us to glean information which was previously thought inaccessible. The Scientific American article [3] talks about potential applications of IFMs, like taking X-ray images without exposing the subject to the deleterious radiation or taking photographs of super-cold (and fragile) Bose-Einstein condensate states which would be destroyed if struck by a photon. The ability to make IFMs with X-rays is still really impractical, though, given that it’s not easy to engineer convenient optical components that work well at such high energies. But even if these ideas are still distant in practical terms, the conceptual underpinnings are there: we at least know how to see without even looking.

References and Further Reading

[1] Elitzur, Avshalom; Vaidman, Lev. “Quantum Mechanical Interaction-Free Measurements.” arXiv:hep-th/9305002v2 (1993).
[2] McDonald, Kirk T. “Ph501 Electrodynamics Problem Set 6.” pp. 6. Princeton University. 2001. http://puhep1.princeton.edu/~kirkmcd/examples/ph501set6.pdf.
[3] Kwiat, Paul; Weinferter, Harald; Zeilinger, Anton. “Quantum Seeing in the Dark.” Scientific American, pp. 72-78. November 1996.
[4] Kwiat, Paul; Weinferter, Harald; Zeilinger, Anton; Kasevich, Mark. “Interaction-Free Measurement.” Phys. Rev. Lett. V. 74, No. 24, pp. 4763-4766. 12 June 1995.
[5] DeWeerd, Alan J. “Interaction-free measurement.” Am. J. Physics 70 (3), pp. 272-275. March 2002.